1.3. El flujo de energía acoplado al ciclo del carbono
De la misma forma que la rueda hidráulica de un antiguo molino era impulsada por un flujo de agua (el río), el ciclo del carbono es impulsado por un flujo de energía. Según muestran las ilustraciones del ciclo del carbono vistas en los epígrafes anteriores, la energía entra en el ciclo en forma de radiación solar, de longitud de onda relativamente corta (entre 0,38 y 0,74 µm), y sale como radiación térmica —calor—, de longitud de onda mucho más larga (en torno a los 12 µm). Esto es, se pasa de una energía concentrada a una energía más dispersa, tal y como estipula la segunda ley de la termodinámica (ver ilustración).
Profundicemos en los detalles del ciclo del carbono concretando cómo ocurre esa dispersión de energía y a qué procesos da lugar. Para Lavoisier, lo importante de la respiración era precisamente que garantizaba el suministro del calor animal. Hoy en día el énfasis se pone en el extremo opuesto: no en la energía que se disipa en forma de calor, sino en la que se recupera para realizar trabajo celular.
Según explicamos en la Unidad 1, la energía que estaba confinada y que, para satisfacer las demandas de la segunda ley de la termodinámica, se dispersaría por un sistema o por su entorno —totalmente si durante el proceso no se efectuara trabajo alguno— es, por definición, la energía libre de ese sistema. La clave del funcionamiento de las células vivas radica en que son capaces de aprovechar una parte de la energía libre para efectuar trabajo, en lugar de permitir que esta se disipe en su totalidad.
Fijémonos, pues, en la variación de energía libre que tiene lugar durante la respiración. Si dejásemos que se disipara totalmente como calor podríamos medirla con un calorímetro, y obtendríamos un valor de 3 012 kJ mol–1 (720 kcal mol–1) en las condiciones típicas de la célula. Esto es, la combinación de una sola molécula de glucosa con seis de O2 libera unos 31,3 eV (véase el recuadro “¿En qué unidades se mide la energía libre?” pulsando el enlace tras la ecuación); podemos esquematizarlo modificando la ecuación (2) de la siguiente forma:
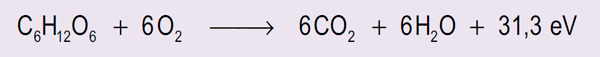 (3) ¿En qué unidades se mide la energía libre?
(3) ¿En qué unidades se mide la energía libre?
¿En qué unidades se mide la energía libre?
- Si nos atenemos a las convenciones del Sistema Internacional, una unidad adecuada para medir la energía libre es el kilojulio por mol (kJ mol–1), siendo un kilojulio (1 kJ) igual a mil julios (1000 J).
- Tradicionalmente, sin embargo, la energía libre se ha medido en kilocalorías por mol (kcal mol–1). Una caloría (cal) es igual a 4,184 J, y una kilocaloría (kcal) son mil calorías —esta unidad se corresponde con la famosa “gran caloría” o Caloría (Cal), con mayúscula, que hasta hace no mucho se utilizaba en dietética—, por lo que 1 kcal mol–1 = 4,184 kJ mol–1; o, a la inversa, 1 kJ mol–1 = 0,239 kcal mol–1.
- A menudo es conveniente referir la energía a moléculas individuales, no a moles. Para ello podríamos simplemente dividir el número de kJ mol–1 por el número de moléculas que hay en un mol (es decir, por el número de Avogadro: NA = 6,022 × 1023), pero las cifras obtenidas resultarían muy pequeñas e inmanejables. Es mejor recurrir a unidades como el electronvoltio (eV), que es la energía adquirida por un electrón al atravesar una diferencia de potencial de un voltio. Se puede demostrar fácilmente que si un mol de una sustancia tiene una energía de 1 kJ, cada una de sus moléculas tendrá, en promedio, una energía de 0,0104 eV. A la inversa, 1 eV por molécula corresponde aproximadamente a 96,485 kJ por mol.
¿En qué tipo de trabajo puede emplear la célula esa energía libre? El más característico es el trabajo químico necesario para formar los miles de glúcidos, proteínas y otras macromoléculas que precisa para crecer y reproducirse. Imaginemos que el proceso —al que en la Unidad 4 denominábamos anabolismo— implica la adición de un átomo tras otro a una pequeña molécula sillar, con la sucesiva formación de enlaces. Entonces se requerirá cierta aportación de energía libre para la formación de cada enlace: entre 0,26 y 0,35 eV en condiciones fisiológicas, dependiendo del tipo concreto (glucosídico, peptídico…); podemos aceptar la cifra de 0,3 eV por término medio.
Por consiguiente, los 31,3 eV liberados al combinar una molécula de glucosa con seis de O2 serían suficientes para formar más de cien enlaces. Pero la energía libre facilitada por una reacción química debe usarse inmediatamente —de lo contrario se disipa en forma de calor—, y resulta altamente improbable que en el instante de la degradación de una molécula de glucosa se “pongan de acuerdo” muchas moléculas diferentes para unirse entre ellas y formar cien enlaces: en general, se formará uno solo. Y eso significaría desperdiciar el 99 por ciento de la energía obtenida de la glucosa.
Una analogía nos ayudará a entender el problema. Supongamos que solo tenemos un billete de cien euros para comprar una barra de pan, y el panadero no tiene cambio. Comprar una sola barra significaría regalar casi todo nuestro dinero; sería más lógico ir al banco y cambiar el billete por otros más pequeños. De igual forma, la molécula de glucosa representa un billete de mucho valor (no económico, sino energético). La pregunta es, entonces: ¿habrá algún modo de “cambiar” la glucosa en “billetes pequeños” o “monedas”, usar los que se precisen para formar enlaces y guardar el resto?
Veremos la respuesta en el siguiente epígrafe.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0
